Små grupper

I matematikken er en gruppe et matematisk objekt med en bestemt struktur. Herunder følger en liste over de endelige grupper med lavest orden (antal elementer) op til gruppeisomorfi.

Listen kan benyttes til at bestemme om en given endelig gruppe G er isomorf på en kendt gruppe ved at bestemme ordenen af G, om G er abelsk eller ej og ordenen af elementerne i G.

Ordliste

• Z_n: Den cykliske gruppe af orden n (ofte benyttes notationen C_n eller Z/nZ).
• Dih_n: Diedergruppen af orden 2n (ofte benyttes notationen D_n eller D_2n).
• S_n: Den symmetriske gruppe af grad n, som indeholder de n! permutationer af n elementer.
• A_n: Den alternerende gruppe af grad n, der indeholder de n!/2 lige permutationer af n elementer.
• Dic_n: Den dicykliske gruppe af orden 4n.

Notationen G × H står for det direkte produkt af to grupper og Gⁿ betegner det direkte produkt af gruppen G med sig selv n gange. G ⋊ H står for det semidirekte produkt, hvor H virker på G; virkningen nævnes ikke, da alle ikketrivielle virkninger giver samme produktgruppe op til isomorfi.

Desuden bemærkes, om grupperne er abelske eller simple. (For grupper af orden n < 60, er de simple grupper præcis de cykliske grupper Z_p, hvor p er et primtal.) Isomorfi betegnes med lighedstegn ("=").

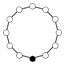
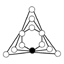
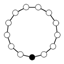
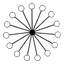
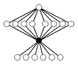
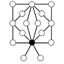
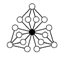
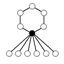
Det multiplikativt neutrale element er i cykelgrafen repræsenteret af den sorte cirkel. Cykelgrafen er en entydig repræsentation for alle grupper med orden mindre end eller lig 16.

I listen af undergrupper er den trivielle gruppe og gruppen selv ikke vist. Når der er flere isomorfe undergrupper, er antallet angivet i parentes.

Små abelske grupper

De endelige abelske grupper kan let klassificeres: De er præcis de cykliske grupper og direkte produkter heraf;

Orden	Gruppe	Undergrupper	Egenskaber	Cykelgraf
1	Den trivielle gruppe = Z1 = S1 = A2	-	Forskellige egenskaber gælder trivielt.
2	Z2 = S2 = Dih1	-	Simpel, mindste ikketrivielle gruppe
3	Z3 = A3	-	Simpel
4	Z4	Z2
	Kleins firegruppe Z2 × Z2 = Dih2	Z2 (3)	Den mindste ikkecykliske gruppe
5	Z5	-	Simpel
6	Z6 = Z3 × Z2	Z3 , Z2
7	Z7	-	Simpel
8	Z8	Z4 , Z2
	Z4 ×Z2	Z2², Z4 (2), Z2 (3)
	Z23	Z2² (7) , Z2 (7)	Pånær det neutrale element svarer elementerne til punkterne i Fanoplanen.
9	Z9	Z3
	Z3²	Z3 (4)
10	Z10 = Z5 × Z2	Z5 , Z2
11	Z11	-	Simpel
12	Z12 = Z4 × Z3	Z6 , Z4 , Z3 , Z2
	Z6 × Z2 = Z3 × Z2²	Z6 (3), Z3, Z2 (3), Z2²
13	Z13	-	Simpel
14	Z14 = Z7 × Z2	Z7 , Z2
15	Z15 = Z5 × Z3	Z5 , Z3
16	Z16	Z8 , Z4 , Z2
	Z24	Z2 (15) , Z2² (35) , Z23 (15)
	Z4 × Z2²	Z2 (7) , Z4 (4) , Z2² (7) , Z23, Z4 × Z2 (6)
	Z8 × Z2	Z2 (3) , Z4 (2) , Z2², Z8 (2) , Z4 × Z2
	Z4²	Z2 (3), Z4 (6) , Z2², Z4 × Z2 (3)

Små ikkeabelske grupper

Orden	Gruppe	Undergrupper	Egenskaber	Cykelgraf
6	S3 = Dih3	Z3 , Z2 (3)	Den mindste ikkeabelske gruppe
8	Dih4	Z4, Z2² (3) , Z2 (5)
	Kvaterniongruppen, Q8 = Dic2	Z4 (3), Z2	Den mindste hamiltonske gruppe
10	Dih5	Z5 , Z2 (5)
12	Dih6 = Dih3 × Z2	Z6 , Dih3 (2) , Z2² (3) , Z3 , Z2 (7)
	A4	Z2² , Z3 (4) , Z2 (3)	Den mindste gruppe, der viser, at en gruppe ikke nødvendigvis har en undergruppe af enhver orden, der går op i gruppeordenen: Der findes ingen undergruppe af orden 6 (se Lagranges sætning og Sylowsætningerne).
	Dic3 = Z3 ⋊ Z4	Z2, Z3, Z4 (3), Z6
14	Dih7	Z7, Z2 (7)
16[1]	Dih8	Z8, Dih4 (2), Z2² (4), Z4, Z2 (9)
	Dih4 × Z2	Dih4 (2), Z4 × Z2, Z23 (2), Z2² (7), Z4 (2), Z2 (11)
	Den generaliserede kvaterniongruppe, Q16 = Dic4
	Q8 × Z2		Hamiltonsk
	Den kvasihedrale gruppe af orden 16.
	Den modulære gruppe af orden 16.
	Z4 ⋊ Z4
	Gruppen frembragt af Paulimatricerne.
	G4,4 = Z2² ⋊ Z4

Fodnote