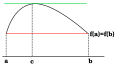
Rolles sætning

I infinitesimalregningen siger den matematiske sætning Rolles sætning, at hvis ${\displaystyle f}$ er en funktion, der er kontinuert på ${\displaystyle [a,b]}$ og differentiabel på ${\displaystyle ]a,b[}$ med ${\displaystyle f(a)=f(b)}$, eksisterer et ${\displaystyle c\in ]a,b[}$ så

${\displaystyle f'(c)=0\;}$.

Sætningen blev først erklæret af inderen Bhaskara i 1150 og siden hen af Michel Rolle i 1691.

Rolles sætning benyttes i beviset for middelværdisætningen, der fjerner kravet, om at ${\displaystyle f(a)=f(b)}$.

Se også

• Middelværdisætningen
• Cauchys middelværdisætning

• Wikimedia Commons har flere filer relateret til Rolles sætning

Spire Denne artikel om matematik er en spire som bør udbygges. Du er velkommen til at hjælpe Wikipedia ved at udvide den.