Pascals trekant

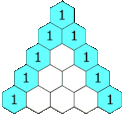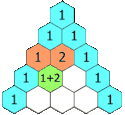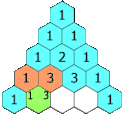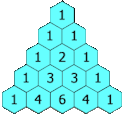
Hvert nummer i en sekskant er summen af de to sekskanter lige over den.

Pascals trekant er et geometrisk arrangement indenfor matematikken. Den har navn efter den franske matematiker Blaise Pascal. Trekanten fremkommer ved at starte med et et-tal øverst, og dernæst for hver række under at starte og slutte med et et-tal. De resterende tal fremkommer ved at tage summen af de to tal, der står umiddelbart ovenover.

Pascals trekant kan, på trods af en meget simpel konstruktionsform, visualisere adskillige matematiske begreber. Hvis vi benævner den øverste række med n=0, den næste række med n=1, osv. Og tilsvarende i hver række benævner tallene fra venstre mod højre med k, hvor det første tal er k=0, så er:

  • Alle tallene i trekanten binomialkoefficienter. , f.eks. for n=5 og k=2: = 10.
  • Summen af tallene i hver række er lig med 2 opløftet i rækkenumrets potens, dvs. 2n
  • Farvelægges tallene i trekanten efter om de er lige eller ulige fremkommer den selvsimilære og fraktale Sierpinski trekant.
  • Venstrestilles trekanten, så vil summen af alle tallene i hver diagonal, fra øverst til højre og ned mod venstre kant i tabellen, generere Fibonacci-talrækken (1, 1, 2, 3, 5, 8, 13, ...).
De første 17 rækker.
En niveau-4 tilnærmelse til Sierpinski trekanten. Opnået ved at farve binomialkoefficienterne hvide hvis de er lige og sort hvis de er ulige.
MatematikSpire
Denne artikel om matematik er en spire som bør udbygges. Du er velkommen til at hjælpe Wikipedia ved at udvide den.

Medier brugt på denne side

Sierpinski Pascal triangle.svg
Forfatter/Opretter: Cmglee, Licens: CC BY-SA 4.0
A level-4 approximation to a Sierpinski triangle obtained by shading the first 32 levels of a Pascal triangle white if the binomial coefficient is even and black otherwise by CMG Lee. For comparison, the colour of the outline of its background is green, blue or purple for the coefficient modulo 3 being 0, 1 or 2, respectively. The text is black, white, red or yellow for the coefficient modulo 4 being 0, 1, 2 or 3, respectively. In the SVG, hover over a number to see its values more clearly.
PascalTriangleAnimated2.gif
Pascal's triangle is a geometric arrangement of integers representing the binomial coefficients in a polynominal equation of the format (x + y)n. The formation also demonstrates many other mathematical properties, such as listing the entire set of the natural numbers in the first diagonal rows. This phenomenon is named after Blaise Pascal in the western world, however was studied in detail before his time in many Asian countries.

It is also called the Halayudha's triangle, in honor of the Sanskrit prosody scholar who described it. (See: Alexander Zawaira and Gavin Hitchcock (2008), A Primer for Mathematics Competitions, Oxford University Press, ISBN 978-0-19-156170-2, page 237)

It is alternately referred to as "Khayyam's triangle" after the Persian Omar Khayyám. Each number is the sum of the two directly above it. This animation shows this relation in the construction of the first five rows, however the pattern applies for an infinite range.

This version has the 1 cells already filled in, and includes actual animation to better demonstrate the construction.
Pascal's Triangle rows 0-16.svg
(c) Nonenmac at engelsk Wikipedia, CC BY-SA 3.0
en:Pascal's triangle. Rows 0 thru 16. Created using Adobe Illustrator and a text editor.