Kvantemekanik

Denne artikel bør gennemlæses af en person med fagkendskab for at sikre den faglige korrekthed.

Kvantemekanik (eller kvantefysik) er en gren af fysikken, som beskæftiger sig med stofs egenskaber på atomart og subatomart niveau. Ud over sin anvendelse inden for fysik og kemi har kvantemekanikken også haft stor betydning for filosofiske emner.

Klassisk mekanik, såsom Newtons love, kan udledes fra kvantemekanik.

Introduktion

Uddybende artikel: Introduktion til kvantemekanik

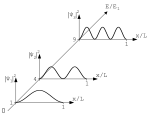
Kvantemekanikken baserer sig på brug af bølgefunktioner til at beskrive partikler.

• 

  Bølgefunktioner for en partikel i en én-dimensionel boks.

• 

  Sandsynlighedstætheder svarende til bølgefunktionerne til venstre.

Ved at beskrive en partikel med bølgefunktion opgiver man det klassiske billede, hvor man altid kan beskrive et atom ved dets placering i rummet, hastighed, retning osv. Al denne information findes nu i partikelrummet, der oftest betegnes med det græske bogstav psi (${\displaystyle \Psi }$).

Max Born indførte fortolkningen af bølgefunktionen som en sandsynlighed. Helt præcist er det kvadratet på bølgefunktionen ${\displaystyle \vert \Psi \vert ^{2}}$, der angiver sandsynligheden for at finde partiklen et bestemt sted i rummet. Her ser man endnu et træk, der tydeligt adskiller kvantemekanikken fra den klassiske fysik. Den klassiske fysik er deterministisk, hvilket vil sige, at hvis man kender al information om et system, så vil man kunne forudsige dens fremtidige udvikling. Ideelt set er der altså ingen usikkerheder i den klassiske fysik. Modsat er kvantemekanikken i sin essens probabilistisk, dvs. baseret på sandsynligheder.

Kvantemekanikken har fået sit navn fra fænomenet kvantisering. Dette betyder, at på mikroskopisk skala sker ændringer i f.eks. energi nogle gange i spring, hvor man klassisk set ville forudsige, at ændringen sker kontinuert. Dette ses bl.a. i et atom, hvor elektronen skifter energiniveau i kvantespring, fordi kun bestemte energiniveau er tilladt. Der findes altså umulige energiniveauer, hvor elektronen ikke kan eksistere, og energiskiftet kan kun ske i diskrete mængder (latin: kvanter).

Historie

Uddybende artikel: Kvantemekanikkens historie

I år 1900 foreslog Max Planck at energi kan være kvantiseret. Denne ide opstod i et forsøg på at beskrive den observerede frekvensfordeling af energi udsendt fra sortlegemer. Einstein forklarede i 1905 den fotoelektriske effekt ved på tilsvarende vis at postulere at lysets energi er kvantiseret. I 1913 forklarede den danske fysiker Niels Bohr brintatomets spektrallinjer ved at antage kvantiserede energitilstande i sin model. Endeligt i 1924 fremførte Louis de Broglie sin teori for stoffets bølgenatur.

Trods deres succes var disse teorier rent fænomenologiske: der var intet fundamentalt argument for kvantisering. Disse teorier kaldes overordnet for den gamle kvantemekanik.

Den moderne kvantemekanik opstod i 1925, hvor Werner Heisenberg udviklede matrixmekanikken, og hvor Erwin Schrödinger udviklede bølgebeskrivelsen med den dertil hørende Schrödinger-ligning. Schrödinger viste efterfølgende at de to tilgange er ækvivalente.

Heisenberg postulerede sit usikkerhedsprincip i 1927. Kvantemekanikken udvikler sig til det, der kendes som Københavnerfortolkningen. I 1927 bliver kvantemekanikken også forenet med den specielle relativitetsteori gennem Paul Diracs ligning. Paul Dirac udviklede ligeledes brugen af operator-algebra i kvantemekanikken – specielt den indflydelsesrige bra-ket notation. I 1932 formulerede John von Neumann en streng matematisk basis for kvantemekanik formuleret som operatorteori.

I 1940'erne blev kvanteelektrodynamikken (QED) udviklet at Richard Feynman, Freeman J. Dyson, Julian Schwinger og Shinichiro Tomonaga som en mere fundamental teori end klassisk elektrodynamik.

Hugh Everett III formulerede mange-verden-fortolkningen i 1956.

Kvantekromodynamikken (QCD) tager sin begyndelse i de tidlige 1960'ere. Teorien, som vi kender den i dag, blev formuleret af Polizter, Gross og Wilzcek i 1975. På baggrund af pionérarbejde af Schwinger, Higgs, Goldstone og andre blev det uafhængigt påvist af Glashow, Weinberg og Salam, at den svage kernekraft og kvanteelektrodynamik kunne forenes i enkelt elektrosvag kraft.

Målingsteori

Uddybende artikel: Kvantemekanisk måling

Et af de områder, hvor kvantemekanikken har haft størst betydning uden for fysikerkredse, er målingsteori.

Superposition

Uddybende artikel: Kvantemekanisk superposition

Når man i kvantemekanikken giver afkald på de klassiske begreber, som position, fart og impuls, åbner man muligheden for at have partikler, der ikke er i en defineret tilstand (eller egentilstand) af f.eks. impuls. Man siger at en sådan partikel er i en superposition af impuls, hvor den populært sagt er i flere tilstande samtidig uden at have valgt hvilken én endnu. Partiklen bliver så at sige først nødt til at vælge i det øjeblik man måler på den, og den antager så straks en defineret tilstand. Når en partikel ikke er i en defineret tilstand, kan man som sagt ikke bruge det klassiske begreb længere, og man er nødt til at arbejde med forventningsværdier. Forventningsværdien er i bund og grund bare middelværdien af de tilstande, som partiklen kan være i.

Det er partiklers superpositionsegenskab, der giver anledning til mange af de fænomener, som kvantemekanikken er berømt for. F.eks. danner superposition grundlaget for kvantecomputeren og for paradokset om Schrödingers kat. Ofte er man også interesseret i at have en partikel i en superposition for at kunne foretage en anden måling præcist, fordi Heisenbergs usikkerhedsrelationer ikke tillader én at kende begge dele på én gang, med fuldstændig nøjagtighed

Stern-Gerlach-eksperimentet

Uddybende artikel: Stern-Gerlach-eksperimentet

Et af kvantemekanikkens mest bizarre resultater kan vises i en tænkt udgave af det forsøg, som Otto Stern og Walther Gerlach lavede i 1922. I det oprindelige eksperiment sendte man en stråle af sølvatomer igennem et inhomogent magnetfelt, hvilket afbøjer atomerne forskelligt alt efter deres elektroners Spin. Når strålen rammer en skærm vil man se to adskilte stråler, fordi elektronerne kan have to spin-tilstande. Dette var i modstrid med den klassiske teori, og eksperimentet dannede et fundamentalt bevis for partiklers spin.

For rigtig at forstå spins bizarre egenskaber kan man tænke sig tre Stern-Gerlach-apparater (S-G) sat efter hinanden. For hvert apparat deler strålen sig i to, og kun den ene fortsætter videre til næste apparat. Det første S-G virker langs z-aksen og deler strålen i to, z+ og z-, hvilket betyder, at de hhv. har spin op og spin ned. Den ene stråle (z+) fortsætter nu ind i det næste S-G, der virker langs x-aksen. Strålen deles igen i to, men denne gang er det efter spin i x-aksens retning: x+ og x- (vi kan kalde det hhv. spin "højre" og spin "venstre"). Til sidst fortsætter kun x+ ind i det sidste S-G, der igen virker langs z-aksen. Overraskende nok kommer der igen to stråler ud af det sidste S-G, der igen er opdelt efter spin op og spin ned.

Klassisk set ville man forvente at der kun kom én stråle med spin op ud til sidst, for alle partikler med spin ned blev frasorteret allerede i første trin. Kvantemekanikkens resultat kan kun tolkes sådan, at man ændrer på partiklens tilstand, når man foretager en måling. Matematisk set betyder det, at man sætter partiklen i en superposition (se ovenfor) af spin op og spin ned, når man foretager målingen i x-aksens retning.

Schrödingers kat

Uddybende artikel: Schrödingers kat

Et af de mest kendte paradokser inden for den moderne fysik handler om Schrödingers kat. Det er et tankeeksperiment, som Erwin Schrödinger fremsatte i 1935. Man forestiller sig, at man har en lukket kasse med en kat, et radioaktivt materiale, en Geigertæller og en beholder med giftgas. Geigertælleren er forbundet med giftgasbeholderen således, at giftgassen frigives, hvis Geigertælleren måler et henfald. Inden for et givet tidsinterval er der altså en vis sandsynlighed for, at det radioaktive materiale henfalder, så katten dræbes. Men hvorvidt katten er levende eller død, vil man ikke kunne afgøre, før man åbner kassen, og dermed kan man betragte katten som værende i en superposition mellem levende og død.

Matematik

Schrödingerligningen

Uddybende artikel: Schrödingerligningen

Den utvivlsomt vigtigste ligning inden for kvantemekanikken er Schrödingerligningen. For én partikel antager ligningen formen

${\displaystyle -{\frac {\hbar ^{2}}{2m}}\nabla ^{2}\Psi \left(\mathbf {r} ,t\right)+U\left(\mathbf {r} ,t\right)\Psi \left(\mathbf {r} ,t\right)=i\hbar {\frac {\partial }{\partial t}}\Psi \left(\mathbf {r} ,t\right)}$,

hvor ${\displaystyle m}$ er partiklens masse, ${\displaystyle \mathbf {r} }$ er stedvektor for partiklen og ${\displaystyle \hbar }$ er Plancks konstant divideret med 2π. Ligningen udtrykker energibevarelse for et kvantemekanisk system – første led på venstre side er det kvantemekaniske udtryk for kinetisk energi, det andet led er den potentielle energi, og højre side angiver den samlede energi for systemet. Schrödingerligningen er en differentialligning, hvis løsninger er funktioner. Man kan bruge den til at finde bølgefunktioner ${\displaystyle \Psi }$, der er løsninger til et givet potential ${\displaystyle U\left(\mathbf {r} ,t\right)}$.

Ligningen findes også i en tidsuafhængig udgave, hvor man kan finde stationære tilstande (eller bundne tilstande), der ikke ændrer sig over tiden. Sådanne tilstande er bl.a. elektroner, der er bundet til en atomkerne, eller andre partikler, der på anden måde er fanget i et elektrisk felt. I den tidsuafhængige udgave erstattes energioperatoren ${\displaystyle i\hbar {\frac {\partial }{\partial t}}}$ på højre side med den samlede energi for systemet ${\displaystyle E}$ og de tidsuafhængige løsninger betegnes ofte med et lille psi (${\displaystyle \psi \left(\mathbf {r} \right)}$).

Ligningen er ikke-relativistisk, dvs. den gælder kun for partikler, hvis hastighed ikke er sammenlignelig med lysets hastighed (299.792.458 m/s). For relativistiske partikler skal man bruge den mere avancerede Dirac-ligning eller kvantefeltteorien.

Dirac-ligningen

Uddybende artikel: Dirac-ligningen

Dirac-ligningen er en fusion mellem Schrödingerligningen og den specielle relativitetsteori. Ligningen er

${\displaystyle -i\hbar c\left({\boldsymbol {\alpha }}\cdot \nabla \right)\psi +\beta mc^{2}\psi =i\hbar {\frac {\partial \psi }{\partial t}}}$,

hvor ${\displaystyle m}$ er partiklens masse, ${\displaystyle \mathbf {r} }$ er stedvektor for partiklen, ${\displaystyle c}$ er lysets hastighed og ${\displaystyle \hbar }$ er Plancks konstant. ${\displaystyle \beta }$ er en 4x4 matrix og ${\displaystyle {\boldsymbol {\alpha }}}$ består af 3 forskellige 4x4 matricer – en for hver dimension. I denne model er ${\displaystyle \psi }$ ikke bare en funktion, men en vektorfunktion med fire komponenter.

En af de ting, som Dirac-ligningen kan forklare, er betydningen af spin. Spin indgår ikke i Schrödingerligningen, men i Dirac-ligningen dukker det op som en konsekvens af mødet mellem kvantemekanik og relativitetsteori. Dirac-ligningen kan forklare ting som finstruktur i atomspektre, men kommer dog til kort ved f.eks. det gyromagnetiske spinforhold ${\displaystyle g_{s}}$. Diracs teori forudsiger værdien af ${\displaystyle g_{s}}$ til at være præcis 2, men målinger viser, at den er lidt højere end 2. Dette kan forklares inden for kvantefeltteori.^[1]

Heisenbergs usikkerhedsrelationer

Uddybende artikel: Heisenbergs ubestemthedsrelationer

Heisenbergs usikkerhedsrelationer er et sæt af uligheder, der er af stor betydning inden for kvantemekanikken. De udtrykker fundamentale grænser for, hvor præcise målinger det er muligt at opnå på samme tid. Mest berømt er uligheden

${\displaystyle \Delta x\cdot \Delta p_{x}\geq {\frac {\hbar }{2}}}$,

der udtrykker, at man ikke kan kende en partikels position og impuls uendeligt præcist på samme tid, fordi de to størrelser er konjugerede variable. Dette skal ikke ses som en begrænsning ved måleudstyret, men en fundamental egenskab ved naturen. Der findes tilsvarende relationer mellem andre variable. Se Heisenbergs ubestemthedsrelationer.

Matematisk kan usikkerhedsprincippet bevises med Fourier-analyse.^[2]

Perturbationsteori

Én af Schrödingerligningens store ulemper er, at den kun kan løses eksakt for nogle ganske simple tilfælde. F.eks. kan man ikke finde analytiske bundne tilstande for andre atomer end hydrogen. Man er derfor nødt til at lave forskellige simplificeringer af de kvantemekaniske problemer for at kunne løse dem. Et af de vigtigste værktøjer til dette er perturbationsteori.

Selv om Schrödingerligningen ikke kan løses eksakt, har den en fordel i at den er lineær. Det betyder, at en lille ændring (perturbation) i potentialet ${\displaystyle U}$ vil give en lille ændring i bølgefunktionen og dens energi. Dermed kan man lave tilnærmede løsninger til avancerede problemer ud fra simple problemer, som man kan løse eksakt.

Se også

• Lene Vestergaard Hau
• atommodel (bølge)
• Kvantecomputer
• Kvantekemi
• Fotonisk krystal
• Nanoteknologi
• Kvantefysisk sammenfiltring
• kvanteteleportation
• Kvantemekanisk tunnelering
• kvanteø (=kvanteprik, nanokrystal, kvantepunkt, kunstigt atom (kvanteø), QD)

Referencer

• Scherrer, Robert (2006). "Quantum mechanics: an accessible introduction". Addison Wesley. ISBN 0-8053-8716-1. (engelsk)

Eksterne henvisninger

• Indledning til Kvantemekanikken (på dansk), Professor Henrik Smith

• Wikimedia Commons har flere filer relateret til Kvantemekanik
• Serge A. Winitzki 1993: Bemærkninger til Mange-Verdener Tolkningen Arkiveret 6. juni 2010 hos Wayback Machine
• Webarchive backup: The Quantum World, EPR:- Spooky Connections (entanglement) Citat: "...Quantum theory upset Einstein because it gave him nothing better to grapple with than frustrating probabilities. In 1936, he got together with Boris Podolsky and Nathan Rosen to create the "EPR paradox". It's ironic that the spooky EPR connection has now been used in the lab to teleport photons, because the original reason for inventing the EPR paradox was to show that one of the implications of quantum theory was so unacceptable that it must be wrong or incomplete in some respect...."
  • 6 November 2003, PhysicsWeb: Mesons violate Bell’s inequality Citat: "...The inequality was violated by three standard deviations in experiments with B mesons at the KEK laboratory in Japan – yet again confirming the predictions of quantum theory..."
  • Number 660 #2, November 4, 2003, Physics News Update: Acceleration Disrupts Quantum Teleportation Arkiveret 19. november 2003 hos Wayback Machine Citat: "...While this effect is small for typical accelerations in Earthly labs the result shows an interesting relationship between the effects of space-time motion and the quantum world..."
• Lydforedrag om kvantemekanik Arkiveret 15. december 2012 hos Wayback Machine ved Benny Lautrup, professor i teoretisk fysik
• Quantum mechanics Arkiveret 11. april 2003 hos Wayback Machine
• Quantum Mechanics Interpretations på Curlie (som bygger videre på Open Directory Project)
  • The Everett Interpretation: many worlds FAQ