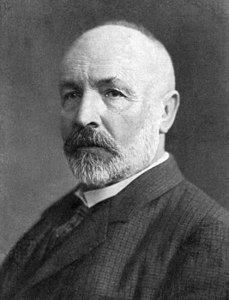Georg Cantor

Georg Cantor
Personlig information
Født	George Ferdinand Ludwig Philipp Cantor 3. marts 1845 Sankt Petersborg, Rusland
Død	6. januar 1918 (72 år) Halle (Saale), Sachsen-Anhalt, Tyskland
Dødsårsag	Hjerteanfald
Nationalitet	Tysk
Bopæl	Tyske Rige, Det Russiske Kejserrige
Søskende	Sophie Nobiling, Constantin Cantor
Ægtefælle	Vally Cantor
Uddannelse og virke
Uddannelses­sted	Humboldt-Universität zu Berlin, Martin-Luther-Universität Halle-Wittenberg
Elev af	Karl Weierstrass
Medlem af	Matematisk Forbund ved Berlins Universitet, Royal Society of Edinburgh (fra 1905), London Mathematical Society (fra 2008), Niedersächsische Akademie der Wissenschaften zu Göttingen, Deutsche Akademie der Naturforscher Leopoldina
Beskæftigelse	Universitetslærer, matematiker, filosof
Fagområde	Mængdelære, matematik
Arbejdsgiver	Martin-Luther-Universität Halle-Wittenberg
Nomineringer og priser
Udmærkelser	Sylvester medaljen (1904)
Information med symbolet hentes fra Wikidata. Kildehenvisninger foreligger sammesteds.  [ redigér på Wikidata ]

Georg Ferdinand Ludwig Philipp Cantor (født 3. marts 1845 i Sankt Petersborg, død 6. januar 1918 i Halle) var en tysk matematiker; professor i Halle.^[1] Hans far var født i Danmark, og moren var russisk.

Han er grundlægger af mængdelæren og kendt for Cantors diagonalbevis.

Arbejdet med Zenons paradoks

Georg Cantor er også kendt for at have forholdt sig kritisk til Zenons paradoks "Achilleus og skildpadden" Han modbeviser Zenons teori om at Achilleus vil komme uendelig tæt på skildpadden, men aldrig nå op på siden af denne. Ifølge Cantor vil en uendelig decimalbrøk, der konvergerer imod et tal (grænseværdien for denne), have samme egenskaber som tallet (grænseværdien) selv og derfor være det selv samme tal. Eksempelvis kan tallet ’5’ også skrives som ’4,9999...’ og tallet ’1’ som ’0,9999...’. Den eneste forskel, ifølge Cantors opfattelse, er notationen. Man afviser altså begrebet om den uendeligt lille størrelse (0,00...1), der netop af Zenon, anses for den evige differens imellem Achilleus og skildpadden.

Når Achilleus således kommer uendelig tæt på skildpadden, er dette det samme som, at han allerede er oppe på siden af den og nu kan passere. Denne løsningsmodel forekommer umiddelbart intuitivt ikke plausibel. De færreste ville nok gå med til at eksempelvis ’0,999...’ er lig med ’1’. På den anden side er det lige så oplagt, at hvis ’X,9999...’=’X+1’ så ville der faktisk være tale om en løsning af Zenons paradoks. Men som det skal vise sig, er sagen lidt mere kompliceret end som så.

Beviset for at 0,999... = 1

Man kan opstille en generel aritmetisk funktion: (10*X-X)/9=X. Man tager et tal, ganger det med ti, trækker 1*X fra summen og dividerer med 9. Så får man igen ’X’. Lad os tage et par eksempler: Lad x være 2: 2 gange 10 er 20, 20 minus 2 er 18, 18/9 er 2. Lad så x være den uendelige decimalbrøk der konvergerer imod tallet 1/3, nemlig 0,333...: 0,333... gange med 10 er 3,333..., 3.333...minus 0,333... er 3, 3/9 er 0.333...(eller 1/3, da 3/9 kan reduceres til 1/3) Således har vi nu tjekket, at denne funktion kan anvendes på såvel naturlige tal som på en uendelig decimalbrøk. Lad os da prøve med en uendelig decimalbrøk, der konvergerer imod et naturligt tal, eksempelvis 0,999...: 0,999... gange med 10 er 9,999..., 9,999... minus 0,999... er 9, 9/9 er l. Med andre ord, hvis vi har at (10*X-X)/9=X så gælder det, at (X=0,999...)=(X=1), hvilket igen kan reduceres til udtrykket 0,999...=1. Således har vi her tilsyneladende et bevis for at en uendelig decimalbrøk, der konvergerer imod et naturligt tal er identisk med sin grænseværdi.

Hvis man er lidt fræk, kan man nøjes med at se på forskellen 1 – 0,999... Lad os holde os til noget, vi kan håndtere, og prøve at beregne 1 – 0,9 først. Det giver 0,1. Så lad os prøve med 1 – 0,99 = 0,01. Ligeledes udregnes 1 – 0,999 = 0,001. Nu er mønsteret tydeligt. Pointen er, at hvis man trækker 0,999... op til n decimaler fra 1, så får man 0,000... med et 1-tal på n'te decimalplads. Trækker man derimod 0,999... fra, dvs. hele den uendelige decimalbrøk, vil man aldrig nogensinde nå til den plads, hvor 1-tallet skal placeres. Deraf sluttes, at 1 – 0,999... = 0.

Referencer

Der er for få eller ingen kildehenvisninger i denne artikel, hvilket er et problem. Du kan hjælpe ved at angive troværdige kilder til de påstande, som fremføres i artiklen.

Eksterne henvisninger

• Wikimedia Commons har flere filer relateret til Georg Cantor

Spire Denne biografi om en tysker er en spire som bør udbygges. Du er velkommen til at hjælpe Wikipedia ved at udvide den.