Mængde

En mængde er en samling af objekter eller elementer, hvor den orden, de optræder i, ikke tillægges en betydning.

Et eksempel på en mængde kunne f.eks. være mængden af almene danske universiteter og kunne angives som {DTU, RUC, AAU, AU, SDU, KU}. Mængden, der ingen elementer indeholder, kaldes den tomme mængde (se nedenfor), mens en mængde med kun ét element kaldes en singleton.

Vi lader ${\displaystyle X}$ betegne en mængde. At et element, ${\displaystyle x}$, tilhører mængden skrives ${\displaystyle x\in X}$ og læses x tilhører X. Eksempelvis tilhører AU førnævnte mængde. Omvendt skrives om et element, ${\displaystyle y}$, der ikke tilhører mængden ${\displaystyle y\notin X}$. Hvis to mængder ${\displaystyle X}$ og ${\displaystyle Y}$ er ens skrives ${\displaystyle X=Y}$, og det gælder, banalt nok, at ${\displaystyle x\in X\Leftrightarrow x\in Y}$. Gælder en betingelse ${\displaystyle S(x)}$ for elementerne i ${\displaystyle X}$ skriver man ${\displaystyle \forall x\in X\mid S(x)}$. Delmængden af en mængde ${\displaystyle X}$ hvis elementer ${\displaystyle x}$ opfylder ${\displaystyle S(x)}$ kan skrives som ${\displaystyle \{x\in X\mid S(x)\}}$; eksempelvis kan mængden bestående af kun de reelle tal -5 og 5 gives ved ${\displaystyle \{x\in \mathbb {R} \mid x^{2}=25\}}$ eller bare ${\displaystyle \{-5,5\}}$.

På samme måde kan man komme ud for at mængder er delmængder af andre mængder. Eksempelvis er {RUC,AU} en delmængde af eksempelmængden med universiteterne. Betegnes den første mængde ${\displaystyle X'}$ og mængden den er en delmængde af ${\displaystyle X}$ skrives at ${\displaystyle X'\subseteq X}$ eller (sjældnere) ${\displaystyle X\supseteq X'}$, hvis og kun hvis ethvert givet ${\displaystyle x\in X'}$ også er indeholdt i ${\displaystyle X}$. Herved gælder følgende relationer (hvor operatoren ${\displaystyle \wedge }$ læses "og"):

${\displaystyle X=Y\Leftrightarrow [X\subseteq Y\wedge Y\subseteq X]}$
og at
${\displaystyle [X\subseteq Y\wedge Y\subseteq Z]\Rightarrow X\subseteq Z}$.

Definitionen på den tomme mængde er givet ved antagelse om, at der findes en mængde ${\displaystyle A}$ og defineret ved ${\displaystyle \emptyset =\{x\in A\mid x\not =x\}}$. Den tomme mængde skrives også ${\displaystyle \{\}}$, som værende en mængde uden elementer. Om den tomme mængde gælder, at den er en delmængde af en hvilken som helst given mængde (inklusiv sig selv).

En mængde, ${\displaystyle M}$ kaldes ordnet, hvis der om elementer, ${\displaystyle x,y\in M}$, gælder enten at ${\displaystyle x<y}$, ${\displaystyle x=y}$ eller ${\displaystyle x>y}$, samtidig med at der for alle ${\displaystyle a,b,c\in M}$ gælder at:

${\displaystyle a<b\land b<c\Rightarrow a<c}$.

Et eksempel på en ordnet mængde er de reelle tal.

Der eksisterer mængder, der er af så stor matematisk betydning og som refereres så ofte til, at de har fået faste navne og symboler. En af disse er den omtalte tomme mængde. Andre specielle mængder inkluderer:

${\displaystyle \mathbb {N} }$ betegner mængden af alle naturlige tal. Altså er ${\displaystyle \mathbb {N} =\{1,2,3,\dots \}}$, og i nogle tilfælde benyttes også ${\displaystyle \mathbb {N} _{0}=\{0,1,2,\dots \}}$.

${\displaystyle \mathbb {Z} }$ betegner mængden af alle hele tal, så ${\displaystyle \mathbb {Z} =\{\dots ,-2,-1,0,1,2,\dots \}}$.

${\displaystyle \mathbb {Q} }$ betegner mængden af alle rationale tal, så ${\displaystyle \mathbb {Q} =\{{\frac {p}{q}}\mid p,q\in \mathbb {Z} ,q\not =0\}}$. Eksempelvis er alle hele tal indeholdt i denne mængde, f.eks. med ${\displaystyle q=1}$.

${\displaystyle \mathbb {R} }$ er mængden af alle reelle tal. Denne mængde er foreningsmængden (se nedenfor) af de rationale tal og de irrationale tal (tal, der ikke kan opskrives som heltalsbrøker, så som π og e)

${\displaystyle \mathbb {C} }$ er mængden af alle komplekse tal.

Alle disse mængder har uendelig kardinalitet, og der gælder, at ${\displaystyle \mathbb {N} \subset \mathbb {Z} \subset \mathbb {Q} \subset \mathbb {R} \subset \mathbb {C} }$.

Ofte har man behov for at konstruere nye mængder ud fra eksisterende. Eksempelvis kan to mængder blive "lagt sammen", idet man danner en mængde, der indeholder alle elementerne fra de to oprindelige mængder. Mængden betegnes foreningsmængden, og foreningsmængden af to mængder ${\displaystyle A}$ og ${\displaystyle B}$ betegnes ${\displaystyle A\cup B}$. Forenes ${\displaystyle n}$ mængder, ${\displaystyle X_{1},X_{2},\dots ,X_{n}}$ benyttes ofte skrivemåden ${\displaystyle \bigcup _{i=1}^{n}X_{i}}$.

Eksempler:

• ${\displaystyle \{1,2\}\cup \{2,3\}=\{1,2,3\}}$
• ${\displaystyle \emptyset \cup \{60\}=\{60\}}$

Lad ${\displaystyle A}$ og ${\displaystyle B}$ være vilkårlige mængder. Da gælder følgende basale egenskaber ved foreningsmængder:

• ${\displaystyle A\cup B=B\cup A}$
• ${\displaystyle A\subseteq B\cup A,B\subseteq B\cup A}$
• ${\displaystyle A\cup A=A}$
• ${\displaystyle A\cup \emptyset =A}$

I analogi med ovenstående hænder det, at man ønsker at betragte mængder, der består af de elementer, flere mængder har til fælles. En sådan mængde kaldes fællesmængden. Fællesmængden af ${\displaystyle A}$ og ${\displaystyle B}$ betegnes ${\displaystyle A\cap B}$, og fællesmængden af mængderne ${\displaystyle X_{1},X_{2},\dots ,X_{n}}$ betegnes ${\displaystyle \bigcap _{i=1}^{n}X_{i}}$.

Eksempler:

• ${\displaystyle \{1,2\}\cap \{2,3\}=\{2\}}$
• ${\displaystyle \{1,2\}\cap \{3,4\}=\emptyset }$

Basale egenskaber ved fællesmængder (hvor ${\displaystyle A'}$ er komplementærmængden til ${\displaystyle A}$):

• ${\displaystyle A\cap B=(A'\cup B')'}$
• ${\displaystyle A\cap B=B\cap A}$
• ${\displaystyle A\cap B\subseteq A,A\cap B\subseteq B}$
• ${\displaystyle A\cap A=A}$
• ${\displaystyle A\cap \emptyset =\emptyset }$

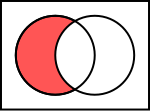
To mængder kan også "trækkes fra hinanden". Den relative komplement til ${\displaystyle A}$ i ${\displaystyle B}$ (også kaldet mængdedifferensen mellem ${\displaystyle B}$ og ${\displaystyle A}$), betegnet ${\displaystyle A\setminus B}$ (eller ${\displaystyle A-B}$) er mængden af alle elementer i ${\displaystyle A}$, der ikke er indeholdt i ${\displaystyle B}$; ${\displaystyle A\setminus B=\{x\in A\mid x\notin B\}}$.

I nogle tilfælde betragtes elementer, der er delmængder af en given universalmængde ${\displaystyle U}$. I disse tilfælde betragtes alle komplementærmængder relativt til universalmængden, og ${\displaystyle U\setminus A}$ kaldes det absolutte komplement eller komplementærmængden til ${\displaystyle A}$ og betegnes ${\displaystyle \complement A}$ eller ${\displaystyle A'}$.

Eksempler:

• ${\displaystyle \{1,2\}\setminus \{3,4\}=\{1,2\}}$
• ${\displaystyle \{1,2\}\setminus \{2,3\}=\{1\}}$
• ${\displaystyle \{1,2\}\setminus \{1,2\}=\emptyset }$

Basale egenskaber ved komplementærmængder:

• ${\displaystyle \complement (\complement A)=A}$
• ${\displaystyle A\cup \complement A=U}$
• ${\displaystyle A\cap \complement A=\emptyset }$
• ${\displaystyle A\subseteq B\Leftrightarrow \complement B\subseteq \complement A}$

Uddybende artikler: Åben mængde og lukket mængde

I topologi og relaterede matematiske emner er det ofte af afgørende karakter, om en betragtet mængde er åben eller lukket. En mængde ${\displaystyle A}$ siges at være åben, hvis ethvert punkt i ${\displaystyle A}$ er et indre punkt (altså at ${\displaystyle \forall a\in A\exists r>0:B_{r}(a)\subseteq A}$). Således fås, at åbne intervaller i ${\displaystyle \mathbb {R} }$, såvel som ${\displaystyle \mathbb {R} }$ selv er åbne mængder. En mængde siges at være lukket, hvis dens komplementærmængde er åben, som det f.eks. gælder for lukkede intervaller i ${\displaystyle \mathbb {R} }$. Herved bliver ${\displaystyle \emptyset }$ og ${\displaystyle \mathbb {R} }$ eksempler på mængder, der både er åbne og lukkede, mens halvåbne intervaller, hverken er åbne eller lukkede.

• Henrik Stetkær, Om uendelighedsbegrebet, 2005
• Ebbe Thue Poulsen, Funktioner af en og flere variable, 2002

Wikimedia Commons har medier relateret til: Mængde