Krypteringsalgoritme

Der er for få eller ingen kildehenvisninger i denne artikel, hvilket er et problem. Du kan hjælpe ved at angive troværdige kilder til de påstande, som fremføres i artiklen.

En krypteringsalgoritme eller chifferskrift^[1] (engelsk: cipher, fransk: chiffre) er en kryptografisk algoritme der entydigt omsætter en besked, klarteksten (eng. plaintext), til krypteret form, chifferteksten (eng. ciphertext), ved hjælp af en nøgle, krypteringsnøglen (eng. encryption key), samt en tilsvarende algoritme der går den modsatte vej. Den første proces kaldes kryptering, den anden dekryptering. Nøglen til de to processer er ikke nødvendigvis de samme. Algoritmen kan være af ikke-matematisk karakter, men er som oftest matematisk.

Med moderne computere har kryptering bevæget sig fra efterretningstjenesternes domæne og ud til almindelige brugere. De fleste e-mail programmer kan sættes op til at kryptere (og/eller signere) den afsendte e-mail. På denne måde kan meddelelsen ideelt set kun læses af den tilsigtede modtager.

Under 2. verdenskrig brugte den tyske marine en kryptografisk algoritme, hvis succes desværre gav årsag til mange skibsforlis, idet ubåde ved hjælp af denne modtog oplysninger om de allieredes bevægelser. Algoritmen hed Enigma, og dette ord er blevet nærmest synonymt for kodesprog til krigsmæssig anvendelse.

Det er en almen misforståelse, at alle krypteringsalgoritmer kan 'knækkes', givet tilstrækkelig tid og computerkraft. Eksempelvis er one-time pad (OTP) kryptering beviseligt umulig at dechiffrere for en tredjepart. Her bruger man en tilfældig nøgle af min. samme længde som klarteksten, og undlader at genbruge denne. Dette er for besværligt til de fleste praktiske anvendelser, men er blevet anvendt i praksis, bl.a. til den "Røde telefon", der forbandt Det Hvide Hus i Washington med Kreml i Moskva.

Klassificering af algoritmer

Blokkryptering vs. stream ciphers

Algoritmer der anvender en fast transformation på blokke af tegn, typisk af en fast længde, kaldes blokkrypteringsalgorimer, modsat stream ciphers, der opererer på en kontinuert strøm af tegn, og med forskellig transformation for hver.

Symmetriske vs. asymmetriske

Symmetriske algoritmer anvender samme nøgle til kryptering og dekryptering. Nøglen må således nødvendigvis være kendt udelukkende af afsender og modtager. Blandt ofte anvendte symmetriske krypteringsalgoritmer er DES, Triple DES (3DES, der bl.a. bruges i Dankort-systemet), IDEA og AES.

Asymmetriske algoritmer (også kendt som public key-algoritmer – offentlig nøgle) anvender to forskellige nøgler til kryptering og dekryptering. RSA-algoritmen er et eksempel på asymmetrisk kryptering. Typisk opdeles de to nøgler i en hemmelig og en offentlig nøgle. Der findes også algoritmer til asymmetrisk kryptering, der benytter sig udelukkende af private nøglepar, men disse er ikke ofte anvendt. Nøgleparret er som Yin og Yang; har den ene nøgle krypteret en bid information, kan kun den anden dekryptere den. Det er bemærkelsesværdigt, at ikke engang den nøgle, der har krypteret informationen, kan dekryptere cifferteksten.

Som navnet "offentlig nøgle kryptering" antyder, er nøglen til krypteringen, typisk offentligt kendt (krypteringsalgoritmerne er typisk altid kendt; det er et generelt princip inden for kryptologien at sikkerheden skal ligge i hemmeligheden af nøglen). Dvs. at alle kan kryptere beskeder vha. algoritmen, men kun personen med den personlige/hemmelige nøgle vil være i stand til at dechiffrere beskederne.

Det kan umiddelbart undre, at asymmetrisk kryptering kan virke. En analogi kan illustrere princippet: A ønsker at kunne modtage en hemmelig leverance fra B. En tredjepart C må ikke kunne få fat i den hemmelige leverance, og når først den er afsendt, må B heller ikke kunne få fat i leverancen. A sender en hængelås til B, men beholder nøglen. B låser leverancen nede i en kasse og sender den til A. A åbner kassen med sin nøgle.

Basale operationer

Klassiske krypteringsalgoritmer samt de fleste moderne symmetriske algoritmer kan beskrives ved en række basale operationer. Moderne symmetriske kryperingsalgoritmer er alle kombinationer af transposition og (typisk polyalfabetisk) substitution.

Transposition

Transposition flytter enheder (f.eks. tegn eller ord) af klarteksten til en anden position, dvs. rækkefølgen af enhederne ændres, men enhederne selv ændres ikke. Matematisk set anvendes en bijektiv funktion på enhedernes positioner. Ved dekryptering foretages blot den modsatte operation. Transpositionen kan være afhængig af krypteringsnøglen, i så fald er denne "opskriften" på transpositionen. Et af de ældste eksempler er skytalen.

Permutation

Permutation er et specialtilfælde af transposition. Her vælger man en permutation af en vis længde, der så anvendes på klarteksten i blokke af denne længde. Jo længere permutationen er, desto sikrere er algoritmen. Teoretisk kan ethver transpositionsalgoritme beskrives som en permutation, men dette er ofte ikke praktisk.

Substitution

Substitution erstatter de enkelte enheder med andre symboler eller enheder efter et fastlagt mønster, dvs. enhederne ændres, men deres positioner gør ikke (modsat transpositionpermutation ovenfor). Ved dekryptering substitueres den modsatte vej. Substitutionen kan være afhængig af krypteringsnøglen, i så fald er denne "opskriften" på substitutionen.

Hvis substitutionen opererer på enkelte tegn kaldes den simpel; hvis der opereres på grupper af tegn kaldes substitutionen polygrafisk. Hvis der anvendes samme substitution på hele klarteksten kaldes substitutionen monoalfabetisk, hvis substitutionen ændrer sig undervejs kaldes den polyalfabetisk. Ved homofonisk substitution anvendes mere en ét symbol for hver enhed i klarteksten for at gøre kryptoanalyse sværere.

Monoalfabetisk substitution: Her erstattes hver bogstav med et andet, f.eks. efter en tabel som denne:

abcdefghijklmnopqrstuvwxyzæøå
SMFKÆQCPHEALGXÅZYWNUBJDRVTIOØ

Således bliver "encyklopædi" til "ÆXFVALÅZIKH". En nemmere måde at anvende substitution er at benytte et kodeord, der skrives først uden at gentage bogstaver, hvorefter man tager de ubenyttede bogstaver i rækkefølge. Således får man ved brug af nøglen "MÅNESKIN":

abcdefghijklmnopqrstuvwxyzæøå
MÅNESKIABCDFGHJLOPQRTUVWXYZÆØ

Har man en lang chiffertekst, kan ren monoalfabetisk substitution brydes med frekvensanalyse. Man finder frekvenserne af ciffertekstens tegn og sammenligner med frekvensfordelingen af alfabetets bogstaver i tekster på det sprog, meddelelsen er skrevet i.

Polyalfabetisk substitution:: Her erstattes det samme bogstav med forskellige bogstaver. F.eks. med tre alfabeter:

abcdefghijklmnopqrstuvwxyzæøå
SMFKÆQCPHEALGXÅZYWNUBJDRVTIOØ
MFOÆZKYRWHCVUDXBEQAÅISNPØGLTJ
XEQMSBLARGJYZOØCPKWDVUINFÅUHÆ

Her bliver "encyklopædi" til "ÆDQVCYÅBUKW" (ved skiftevis at bruge de tre alfabeter).

Eksempler på krypteringsalgoritmer

Cæsaralgoritmen

Cæsaralgoritmen flytter hvert bogstav et antal pladser ned i alfabetet. Eksemplet viser et skift på tre pladser, således at et B i klarteksten bliver til et E i cifferteksten.

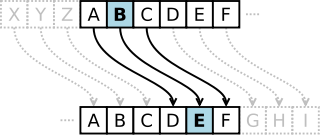
Cæsaralgoritmen er et specialtilfælde af monoalfabetisk substitution, som blev benyttet under Julius Cæsar. Hvert bogstav erstattes med et bogstav et antal pladser længere nede i alfabetet (shift cipher). Nøglen er antallet af pladser der flyttes.

Et shift cipher for det danske alfabet er givet ved

• e(x) = x+K modulo 29
• d(x) = x-K modulo 29

F.eks. i teksten "cæsar" med K=3 bliver "c" til "F", "æ" til "A" osv., hvilket giver teksten: "FAVDU". Cæsaralgoritmen brydes relativt let ved frekvensanalyse.

Vigenère

Et tabula recta til brug for Vigenèrealgoritmen

Vigenèrealgoritmen er det bedst kendte eksempel på polyalfabetisk substitution. Det blev udviklet af den franske diplomat Blaise de Vigenère. Her vælges et ord som nøgle, og hvert bogstav i nøglen bruges skiftevis til at vælge en substitutionstabel. Typisk benyttes et tabula recta (se illustration), hvilket betyder at alle substitutionstabeller svarer til en Cæsaralgoritme (se ovenfor). Er kodebogstavet f.eks. "E", benyttes en cæsaralgoritme med et skift på fire pladser. Et eksempel med nøglen "VIGENERE":

Klartekst:    angribveddaggry
Nøgle:        VIGENEREVIGENER
Chiffertekst: VVMVVFMIYLGKTVP

Bemærk at hele fem bogstaver krypteres til V, mens de to d'er i klarteksten krypteres forskelligt.

Vigenèrealgoritmen blev i flere hundrede år blev anset for ubrydelig; så sikkert, at man gav det navnet "Le carré indéchiffrable" – det ubrydelige kvadrat. Algoritmen kan imidlertid brydes ved først at lave en Kasiski test, der fastlægger længden af nøglen. Derefter benyttes frekvensanalyse på de bogstaver i chifferteksten der er oversat med det samme bogstav i nøglen.

Enigma

Enigma er en elektromekanisk krypteringsmaskine, som anvender polyalfabetisk substitution. Den blev udviklet af tyskeren Arthur Scherbius (patenteret i 1918). Maskinen var i forskellige udgaver rygraden i de tyske krypteringssystemer under Anden Verdenskrig. Den mest sofistikerede type anvendtes af den tyske ubådsflåde. Briterne indrettede på Bletchley Park et kodebrydningscenter under ledelse af Alan Turing, som havde held og begavelse til at bryde koden.

DES og Triple DES

Data Encryption Standard (DES) blev udviklet af IBM i 1977. DES er i dag en af de mest benyttede symmetriske krypteringsmetoder. Ved denne kryptering bliver klarteksten først opdelt i blokke på hver 64 bits (8 bytes). Nøglen indeholder også 64 bits, hvoraf 8 bits er paritetsbits, så nøglen reelt er på 56 bits. Hver tekstblok gennemgår en kompliceret række af transformationer sammen med nøglen.

I Triple DES anvendes DES tre gange med forskellige nøgler; først krypteres med den første nøgle, herefter dekrypteres med den anden nøgle, og til sidst dekrypteres med den tredje nøgle. Triple DES bruges bl.a. i Dankort-systemet.

AES

Advanced Encryption Standard (AES) anvender symmetriske nøgler og vil erstatte den meget anvendte Data Encryption Standard (DES). AES er baseret på den vindende algoritme i en konkurrence udskrevet af de amerikanske myndigheders National Institute of Standards and Technology (NIST) i 1997 og som sluttede i år 2000. Algoritmen der vandt, Rijndael, er udviklet af to belgiske krypteringseksperter, Vincent Rijmen og Joan Daemen.

RSA

RSA er formodentlig den mest anvendte asymmetriske krypteringsalgoritme. Systemet virker ved at vælge to (store) primtal p og q, hvorfra man beregner n = pq samt d og e, hvor de mod (p-1)(q-1) = 1, og e og (p-1)(q-1) ikke har fælles primtalsfaktorer. (n,e) er den offentlige nøgle, (n,d) er den private/hemmelige nøgle. Kryptering af tallet m foregår herefter ved at beregne c = m^e mod n. Dekryptering udføres ved at beregne m = c^d mod n.

Sikkerheden i systemet hviler på antagelsen om at primtalsfaktorisering er et "svært" problem, dvs. at der ikke findes algoritmer der kan udføre opgaven i polynomiel tid. RSA kan dog brydes i polynomiel tid på en kvantecomputer med Shors algoritme.

PGP

PGP (Pretty Good Privacy) er et krypteringsprogram udviklet af Philip Zimmermann i 1991 og er en standard for kryptering af e-post. Programmet er af meget høj kvalitet, og har udløst utallige juridiske problemer mellem Phil Zimmermann og NSA. Systemet er en kombination af asymmetrisk og symmetrisk kryptering, hvor den asymmetriske kryptering benyttes til at kryptere en længere (tilfældigt genereret) symmetrisk nøgle, der vedlægges beskeden. Grunden til denne tilgang er at asymmetrisk kryptering er meget langsommere end symmetrisk kryptering.

Diverse noter

• Af sikkerhedsgrunde er det ofte hensigtsmæssigt at komprimere data inden kryptering, idet redundans vil give en tredjepart bedre mulighed for at bryde krypteringen.
• Kryptering bliver sjældent brudt pga. svagheder i selve algoritmen. Oftest drejer det sig om fejl i implementeringen eller andre menneskelige fejl.
• En kryptografisk algoritmes styrke skal typisk måles mod omkostningen ved at bryde den i bredeste forstand. Således er omkostninger den "billigste" af flere muligheder, der ud over at finde fejl i algoritmen og benytte brute force angreb, omfatter at finde personen der kender nøglen og tvinge den ud af ham/hende.

Referencer